Accurate Lunar Grazing Occultation Analysis (C) 2019 John Irwin

Accurate Lunar Grazing Occultation Analysis

Below I report on the results of my analysis of two sets of high-quality grazing observations recorded by Tim Haymes (UK) in 2017 and 2015. These reductions use a more sophisticated modelling of the occultations than you would normally see from mainstream analysts and I would like to highlight how it is possible to achieve a similar accuracy by making a simple change to the way ephemeris calculations are performed.

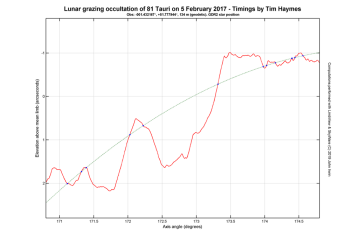
The following two images show the star tracks across the lunar limb, with points locating the position of the star on the lunar limb plane at the observed times. The axes have been oriented to present a natural view of each occultation, where the 2017 events took place at the southern limb while the 2015 events occurred at the northern limit. The plots show an almost perfect alignment between the observed star positions and the true lunar limb.

A text file is also available detailing the numerical results.

81 Tauri	SAO 109080

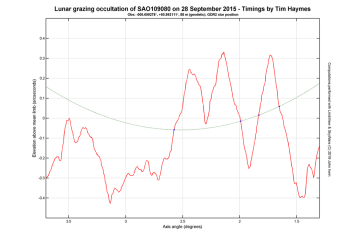Follow the image links to see full-sized versions of each plot.

In terms of the mean and standard deviation of the residuals (see results file), we have (+3.0 ± 4.2) mas for the 81 Tauri occultation. For the SAO 109080 occultation the residuals are similar at (–2.0 ± 7.2) mas. These would appear to be excellent results.

To achieve this sort of accuracy I took account of things like: (1) UT1-UTC and polar motion, (2) the observer's geodetic elevation (above the WGS84 reference ellipsoid) rather than the orthometric elevation (above mean sea level), (3) the actual topocentric lunar libration, including the range, in the generation of the limb profile, and of course (4) Gaia data for the star. But a large contribution to the accuracy can be attributed to the use of planetary aberration in the calculation of the apparent position of the Moon, where commonly stellar aberration would have been used.

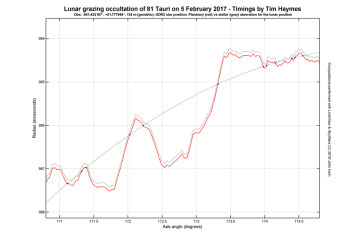
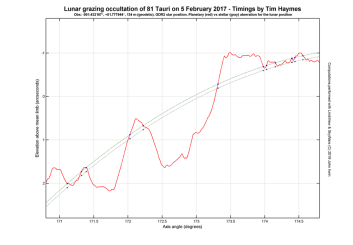
Why would this make a big difference? Simply because in the calculation of the apparent position of the Moon, stellar aberration merely performs a rotation (change of direction) of the astrometric (light-time adjusted) position. So the range to the Moon does not change and this will result in a miscalculation of the apparent size of the lunar limb. Planetary aberration does not suffer from this limitation because it deals with the actual 3D position of the Moon, not just its direction, so it can naturally account for the distance to the Moon.

The following two plots illustrate this effect for the 81 Tauri occultation.

The first plot compares the lunar limbs calculated using planetary and stellar aberration in absolute terms. The vertical axis is now in arcseconds from the centre of the Moon rather than relative to the mean limb. You can see that the limb for stellar aberration is smaller than that for planetary aberration and the displacement is strictly vertical, i.e. radial. This is all consistent with the fact that stellar aberration has overestimated the lunar range, as the following data will show, where R is the apparent topocentric range of the Moon and SD is the corresponding semidiameter of the mean limb:

T = 19:17:12 UTC

Planetary aberration: R = 363844.678 km, SD = 985.3335"
  Stellar aberration: R = 363878.471 km, SD = 985.2420"

This means the lunar range is 33.8 km greater for stellar aberration, giving an apparent semidiameter which is 91.5 mas smaller.

Also, if the analysis of the observations is done with the smaller lunar limb, the residuals shoot up to (+94.5 ± 4.2) mas. Thus the residuals have increased by 94.5 – 3.0 = 91.5 mas, which is entirely consistent with the change in the semidiameter.

In the other plot I've again shown the limbs and star tracks relative to their respective mean limbs. The limb shapes are virtually identical and completely overlap, but there is now a displacement of the star track, which helps us see more clearly the discrepancy resulting from the use of stellar aberration.

For the SAO 109080 occultation, we find that the effect of using stellar aberration in place of planetary aberration is much reduced:

T = 02:32:01 UTC

Planetary aberration: R = 353695.047 km, SD = 1013.6089"
  Stellar aberration: R = 353696.387 km, SD = 1013.6051"

Thus the lunar range is only 1.3 km greater for stellar aberration, giving a semidiameter which is 3.8 mas smaller. This is also reflected in the increase of the residuals from –2.0 to +1.9 mas. So stellar aberration seems to do a good job of reproducing these observations.

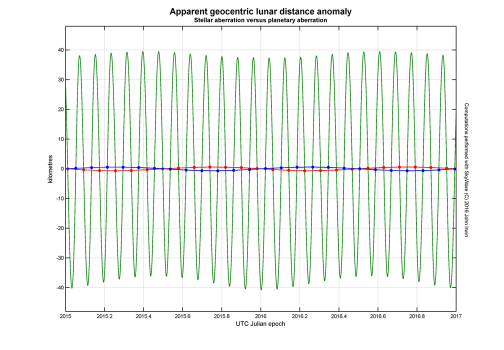
Now, there is a very good reason for this behaviour: The range discrepancy between planetary and stellar aberration is known to be minimal near the times of New and Full Moon and SAO 109080 was occulted during a total lunar eclipse. The image below demonstrates the time-dependence of the range discrepancy relative to the centre of the Earth over a period of two years, where the blue and red points locate the times of New and Full Moon.

You can see that the magnitude of the discrepancy can reach up to ~40 km which is enough to change the semidiameter by more than 100 mas, if the Moon should find itself near perigee (worst case scenario). This is quite a substantial change and suggests we should account for it in our reductions of lunar occultations, especially grazing ones, and avoid a potentially large systematic error caused by an inadequate modelling of the lunar distance.

First published 24 May 2019